最近登場した個人戦CTFプラットフォームであるAlpacaHackで、Crypto回があったので参加しました。一回6時間、4問だけの出題で気軽に挑戦できるので良いですね。adminやauthorは国内CTFプレイヤーで上から数えても五指か十指かそのくらいにはいる実力者で問題の質も保証されているので、入門者にも*1経験者にも、私のような「昔やってました」という人にもおすすめです。
出るかどうか迷ってたけど寝坊しつつもいい感じの時間に起きられたので出て、2時間40分55秒で全完して10位でした。上振れも下振れもしない、実力程度の順位かな〜と思います。

以下writeup。AlpacaHackにはCTF始めたての人もたくさん参加していると思うので(参加してくれていると嬉しいので)、どういうことを考えていた、とかも頑張って書きます。
qrime
問題名みて「primeのpがqになってるやつ〜! RSAで かな〜」と思いながら見たら、ちょっと違った。RSAで
の素因数
が次の関数で生成されていた。
def gen(): while True: q = getRandomNBitInteger(256) r = getRandomNBitInteger(256) p = q * nextPrime(r) + nextPrime(q) * r if isPrime(p) and isPrime(q): return p, q, r
雑に読むと、「は適当な素数で、
はランダムな値。
と書いて
は素数で、
」ということがわかる*2。ここで
は適当な小さい整数
をつかって
と表せるような素数で、記号は適当に導入した。
で、問題はとRSAで暗号化された
が与えられているというやつ。明らかに
の作り方が変で、ヒントの
ももらえているので、
をを素因数分解する系の問題でしょう、ということにはあたりがつく。
で、まずは適当に導入した記号を使いつつを開いていく。
すると(は小さいことがわかってて全探索すればよいので)
が
の2変数で表されることがわかって、
は既知だから
について解いたらよいね、ということがわかる。
わかるけど、競技中の私は「あ〜あきらかにだね〜、じゃあ
って近似できて
って変形すれば
の近似値が取れそう〜って言って解きました。
こう。近似した後ちゃんとしたの値になるかどうかは、近似値に適当な値を足したり引いたりして
を割り切れるかで判定した。
from Crypto.Util.number import isPrime from gmpy2 import iroot n=2006...7779 e=65537 c=7716...708 r=307...5270 # n = 2*q**2*r + q**2*a + q*r*b # -> n / (2*r) ~ q**2 qq, _ = iroot(n // (2*r), 2) for diff in range(-200, 200): q = qq + diff if isPrime(q) and n % q == 0: p = n // q phi = (p - 1) * (q - 1) d = pow(e, -1, phi) m = pow(c, d, n) print(bytes.fromhex(hex(m)[2:])) quit()
Rainbow Sweet Alchemist
何を言ってるかはわからないけど、Acronym的にRSAということだけがわかる。
で、ちゃんとスクリプトを読みはじめるとまず r = random.Random(0) と書いてあって「あ〜これランダムと言いつつ値が固定されてるやつじゃん〜」になる。さらに真面目に読むと、RSAで、の作り方が次のように独特であることがわかる。
deterministicGetPrimeは呼び出すたびに異なる素数を返す関数- これで適当に素数を集めて
factorsとして、全部掛けて+1したあたいが素数ならその素数があるいは
になる
- もし素数じゃなかったら
factorsからランダムな値を抜いて、別にランダムな素数をfactorsに1個追加してもう一回試す、というのをやる
先述の r = random.Random(0) によって、determinisitcGetPrimeの回目の呼び出しの値はわかる。一方
factorsからどの値が抜かれるか、というのは固定されてない乱数生成器がつかわれていてわからない、という問題。
まず一瞬考えるのは「determinisitcGetPrimeが返す素数は全部わかるわけだからfactorsから何が抜かれたらどうなる、を全部シミュレーションしたら良いんじゃね」ということだが、面倒だからやらなかった。
かわりに考えたのは、「(
)は
という形式で、どの
も64bitだから、
はB-smoothな値なんだなぁ」ということ。要するに
の素因数がある程度小さい値に限られるということで、こういうケースではpollard's p-1 methodという素因数分解方法が有効*3。
が、実際には拾ってきたp-1法をやってみてもうまくいかなくて、もうちょい工夫する必要がある。
p-1法についてはこのエントリとかにかいてあって、私は良く知らないが、読んでみると適当なにたいして
のあらゆる素因数(の候補)の積
があって
が
の素因数を計算できるらしい。
普通のp-1法ではp-1の素因数にどういう値が入ってくるかはわからないので小さい素因数から順番にに掛けまくるわけだが、今回は素因数の生成は決定的なので、
に含まれるべき素因数の候補は列挙できる。ので列挙してp-1法をやると良いです。
つまりこういう感じ↓
import math import random from Crypto.Util.number import isPrime r = random.Random(0) def deterministicGetPrime(): while True: if isPrime(p := r.getrandbits(64)): return p def pollard(n): a = 2 while True: x = deterministicGetPrime() a = pow(a, x, n) d = math.gcd(a - 1, n) if 1 < d < n: return d n=235...1909 e=65537 c=945...459 p = pollard(n) assert p is not None q = n // p phi = (p - 1) * (q - 1) d = pow(e, -1, phi) m = pow(c, d, n) print(bytes.fromhex(hex(m)[2:]).decode())
典型というか、既存のアルゴリズム(が動く原理)についてちゃんと理解しているとそのアルゴリズムを改造して解けるという面白い問題だった。私はB-smooth→p-1法 の対応だけ暗記しててp-1法については解きながら調べてあとはスクリプトキディしました、ということ
A Dance of Add and Mul
ここからコードの細かい解説をサボります。面倒なので……。
BLS12-381という楕円曲線があって、その生成元をとする*4。
フラグを1bitずつ暗号化していて、その方法はこう↓。というのは乱数列。
- 暗号化したいbit
が0のとき:
- 暗号化したいbit
が1のとき:
で、なんかの暗号化にも
の暗号化にも
が登場するので、となりあうbitの暗号化結果はなんらかの関連がありそうとわかる。もうちょい考えると、例えば
だったとして、それぞれを暗号化したとき
で、どちらにもという項が登場していて、差をとったら消せそう〜ということがわかる。さらに他のケースについても考えると次のようになる。
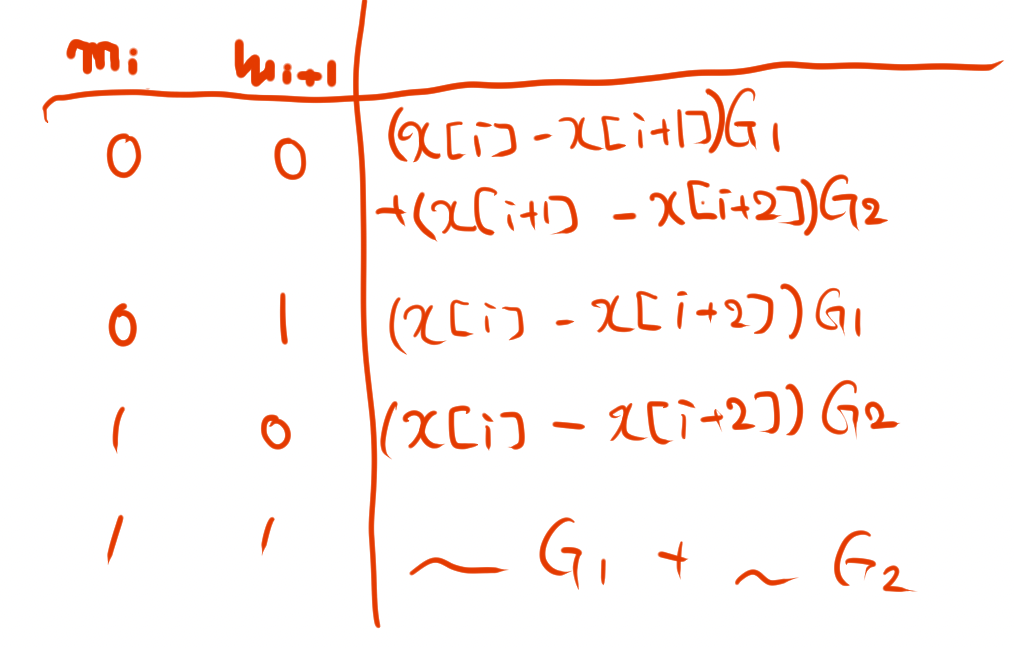
つまり、を考えて、これが
の倍数なら
だし、
の倍数なら
だし、そのどちらでもなければ、
ということがわかる。
あとは が
や
の倍数か調べる方法がわかれば良くて、これはBLS12-381という文字列を見た瞬間にペアリングのことを連想すれば良い。
ペアリングは(同一の曲線上に限らない)楕円曲線の点2点をとってなんか数値を計算する演算で、同じ巡回群の元を渡すと1になるという性質がある。つまりペアリングの演算として
とか
とかを計算して、1になったら
の倍数だねといえる。
で、こういう感じで解いた
import os import random from Crypto.Util.number import bytes_to_long import ast # BLS12-381 curve p = 0x1a0111ea397fe69a4b1ba7b6434bacd764774b84f38512bf6730d2a0f6b0f6241eabfffeb153ffffb9feffffffffaaab K = GF(p) E = EllipticCurve(K, (0, 4)) G1, G2 = E.gens() o1, o2 = G1.order(), G2.order() cs = ast.literal_eval(open("chall.txt").read()) cs = [E(c) for c in cs] last = 0 ms = ["0"] for i in range(len(cs) - 1): R = cs[i] - cs[i + 1] is_g1 = G1.weil_pairing(R, o1) == 1 is_g2 = G2.weil_pairing(R, o2) == 1 if not is_g1 and not is_g2: # ms[i] and ms[i+1] are same # last is inherited pass elif not is_g1 and is_g2: # ms[i] == 1 and ms[i+1] == 0 last = "0" elif is_g1 and not is_g2: # ms[i] == 0 and ms[i+1] == 1 last = "1" else: assert False, "unreachable" ms.append(last) print(int("".join(ms), 2))
Hat Trick
「ローリングハッシュだ〜。keymoon、競技プログラマでAlpacaHack(の特にCrypto)やってる人が多いからそれ向けの問題だしてるな〜」と思いながら、問題を眺めた。
ローリングハッシュときたらLLLというところまでは連想ゲームなので説明できなくて、解くときにrkm0959というひとがライブラリ化したCVP solverであるところのInequality Solving with CVPが便利ということをご紹介。
このライブラリはCVPを解くときに条件を書いたらLLLのための行列はいい感じにやってくれるというやつで、非常に便利に使える。制約の配列と下限・上限の配列を作って渡してやれば良くて、今回の問題であれば次のようにそれぞれの配列を作っていく。
まず求めたい未知変数について考える。今回 と
を満たす
を求めたら良い。LLLではmodを含む式はmodの部分を整数係数
を使って開くので
と変形することを考えると、
も未知変数と言える。
続いて制約をつくっていく。制約は式の左辺を表す配列と、その上限・下限となる値の3つの組からなる。制約は複数あるのが普通で、今回であればローリングハッシュの計算結果を所望の値にするという制約と、各文字が英小文字の範囲に入るという制約を表現する必要がある。
まず1個目のローリングハッシュの値についての制約を作る。式の左辺を表す配列は、番目の要素には未知変数の
番目の変数にかける係数を入れて作ればよい。今回は
となる(1個目のローリングハッシュについて考えるときは2, 3個目のローリングハッシュのための変数
k2, k3は無視したいので、係数0をかける)。これでが表現できた。そしてこの式をどのような上限・下限で挟むかを決めるが、今回は
にぴったり一致させたいので上限も下限もこの値にする。
続いて2個目、3個目のローリングハッシュの値についての制約も同様に別の配列と上限・下限の値として作る。
更に個別の値の制約、の部分も作る。
に対応する式の配列は
であり、
に対応する式の配列は
である。そして、これの上限と下限は当然
ord('z')と ord('a') になる。
これですべての制約を表現できたので、あとはこれをsolveという関数に突っ込んでやれば良い。式の制約はMという行列(の転置)で表され、上限・下限はlb, ub*5という配列に入っている
# [c1, c2, ..., cN, k1, k2, k3] M = matrix(ZZ, [ # hash bounds [params[i]["base"]**j for j in range(N)] + [0 for _ in range(i)] + [params[i]["p"]] + [0 for _ in range(len(params) - i - 1)] for i in range(len(params)) ] + [ # character bounds [0 for _ in range(i)] + [1] + [0 for _ in range(S - i - 1)] for i in range(N) ]) lb = target + [ord('a') for _ in range(N)] ub = target + [ord('z') for _ in range(N)] load("./rkm.sage") _, _, solution = solve(M.T, lb, ub)
この問題を解くスクリプト全体はいかのようになる
from ptrlib import Socket import string import ast MAX_LEN = 54 class RollingHash: def __init__(self, p=None, base=None) -> None: self.p = getPrime(64) if p is None else p self.base = (getRandomInteger(64) if base is None else base) % self.p def hash(self, s: str): res = 0 for i, c in enumerate(s): res += ord(c) * (self.base ** i) res %= self.p return res def check_str(s: str, max_len: int): assert len(s) <= max_len, "too long!" for i, c in enumerate(s): assert c in string.ascii_lowercase, f"found invalid char {c} at {i}" sock = Socket("nc 34.170.146.252 53764") params = ast.literal_eval(sock.recvlineafter("params: ").decode().strip()) h = [RollingHash(p=param["p"], base=param["base"]) for param in params] for _ in range(3): line = sock.recvline() if b"target: " not in line: quit() target = ast.literal_eval(line[len("target: "):].decode().strip()) N = MAX_LEN S = N + len(params) # [c1, c2, ..., cN, k1, k2, k3] M = matrix(ZZ, [ # hash bounds [params[i]["base"]**j for j in range(N)] + [0 for _ in range(i)] + [params[i]["p"]] + [0 for _ in range(len(params) - i - 1)] for i in range(len(params)) ] + [ # character bounds [0 for _ in range(i)] + [1] + [0 for _ in range(S - i - 1)] for i in range(N) ]) lb = target + [ord('a') for _ in range(N)] ub = target + [ord('z') for _ in range(N)] load("./rkm.sage") s = "".join([chr(c) for c in solution[:N]]) print(s) # check for i in range(len(params)): assert h[i].hash(s) == target[i], f"hash mismatch at {i}" check_str(s, MAX_LEN) sock.sendlineafter("> ", s) sock.interactive()